pgr_degree - pgRouting Manual (3.8)

Edges

example :

Get the degree of the vertices defined on the edges table

SELECT * FROM pgr_degree($$SELECT id, source, target FROM edges$$)
ORDER BY node;
 node  degree
------+--------
    1       1
    2       1
    3       2
    4       1
    5       1
    6       3
    7       4
    8       3
    9       1
   10       3
   11       4
   12       3
   13       1
   14       1
   15       2
   16       3
   17       2
(17 rows)

Edges and Vertices

Example :

Extracting the vertex information

pgr_degree can use pgr_extractVertices embedded in the call.

For decent size networks, it is best to prepare your vertices table before hand and use it on pgr_degree calls. (See Using a vertex table )

Calculate the degree of the nodes:

SELECT * FROM pgr_degree(
  $$SELECT id FROM edges$$,
  $$SELECT id, in_edges, out_edges
    FROM pgr_extractVertices('SELECT id, geom FROM edges')$$);
 node  degree
------+--------
    1       1
    2       1
    3       2
    4       1
    5       1
    6       3
    7       4
    8       3
    9       1
   10       3
   11       4
   12       3
   13       1
   14       1
   15       2
   16       3
   17       2
(17 rows)

Edges SQL

For the Edges and Vertices signature:

For the Edges signature:

Vertex SQL

For the Edges and Vertices signature:

Degree of a loop

A loop contributes 2 to a vertex’s degree.

Using the Edges signature.

SELECT * from pgr_degree('SELECT 1 as id, 2 as source, 2 as target');
 node  degree
------+--------
    2       2
(1 row)

Using the Edges and Vertices signature.

SELECT * FROM pgr_degree(
  $$SELECT 1 AS id$$,
  $$SELECT id, in_edges, out_edges
     FROM pgr_extractVertices('SELECT 1 as id, 2 as source, 2 as target')$$);
 node  degree
------+--------
    2       2
(1 row)

Degree of a sub graph

For the following is a subgraph of the Sample Data :

• \(E = \{(1, 5 \leftrightarrow 6), (1, 6 \leftrightarrow 10)\}\)

• \(V = \{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17\}\)

The vertices not participating on the edge are considered isolated

• their degree is 0 in the subgraph and

• their degree is not shown in the output.

Using the Edges signature.

SELECT * FROM pgr_degree($$SELECT * FROM edges WHERE id IN (1, 2)$$);
 node  degree
------+--------
   10       1
    6       2
    5       1
(3 rows)

Using the Edges and Vertices signature.

SELECT * FROM pgr_degree(
  $$SELECT * FROM edges WHERE id IN (1, 2)$$,
  $$SELECT id, in_edges, out_edges FROM vertices$$);
 node  degree
------+--------
    5       1
    6       2
   10       1
(3 rows)

Using a vertex table

For decent size networks, it is best to prepare your vertices table before hand and use it on pgr_degree calls.

Extract the vertex information and save into a table:

CREATE TABLE vertices AS
SELECT id, in_edges, out_edges
FROM pgr_extractVertices('SELECT id, geom FROM edges');
SELECT 17

Calculate the degree of the nodes:

SELECT * FROM pgr_degree(
  $$SELECT id FROM edges$$,
  $$SELECT id, in_edges, out_edges FROM vertices$$);
 node  degree
------+--------
    1       1
    2       1
    3       2
    4       1
    5       1
    6       3
    7       4
    8       3
    9       1
   10       3
   11       4
   12       3
   13       1
   14       1
   15       2
   16       3
   17       2
(17 rows)

Dry run execution

To get the query generated used to get the vertex information, use dryrun => true .

The results can be used as base code to make a refinement based on the backend development needs.

SELECT * FROM pgr_degree(
  $$SELECT id FROM edges WHERE id < 17$$,
  $$SELECT id, in_edges, out_edges FROM vertices$$,
  dryrun => true);
NOTICE:
    WITH

    -- a sub set of edges of the graph goes here
    g_edges AS (
      SELECT id FROM edges WHERE id < 17
    ),

    -- sub set of vertices of the graph goes here
    all_vertices AS (
      SELECT id, in_edges, out_edges FROM vertices
    ),

    g_vertices AS (
      SELECT id,
        unnest(
          coalesce(in_edges::BIGINT[], '{}'::BIGINT[])
          
          coalesce(out_edges::BIGINT[], '{}'::BIGINT[])) AS eid
      FROM all_vertices
    ),

    totals AS (
      SELECT v.id, count(*)
      FROM g_vertices v
      JOIN g_edges e ON (v.eid = e.id) GROUP BY v.id
    )

    SELECT id::BIGINT, count::BIGINT FROM all_vertices JOIN totals USING (id)
    ;
 node  degree
------+--------
(0 rows)

Finding dead ends

If there is a vertices table already built using pgr_extractVertices and want the degree of the whole graph rather than a subset, it can be forgo using pgr_degree and work with the in_edges and out_edges columns directly.

The degree of a dead end is 1.

To get the dead ends:

SELECT id FROM vertices
WHERE array_length(in_edges  out_edges, 1) = 1;
 id
----
  1
  2
  5
(3 rows)

A dead end happens when

• The vertex is the limit of a cul-de-sac, a no-through road or a no-exit road.

• The vertex is on the limit of the imported graph.

  • If a larger graph is imported then the vertex might not be a dead end

Node \(4\) , is a dead end on the query, even that it visually looks like an end point of 3 edges.

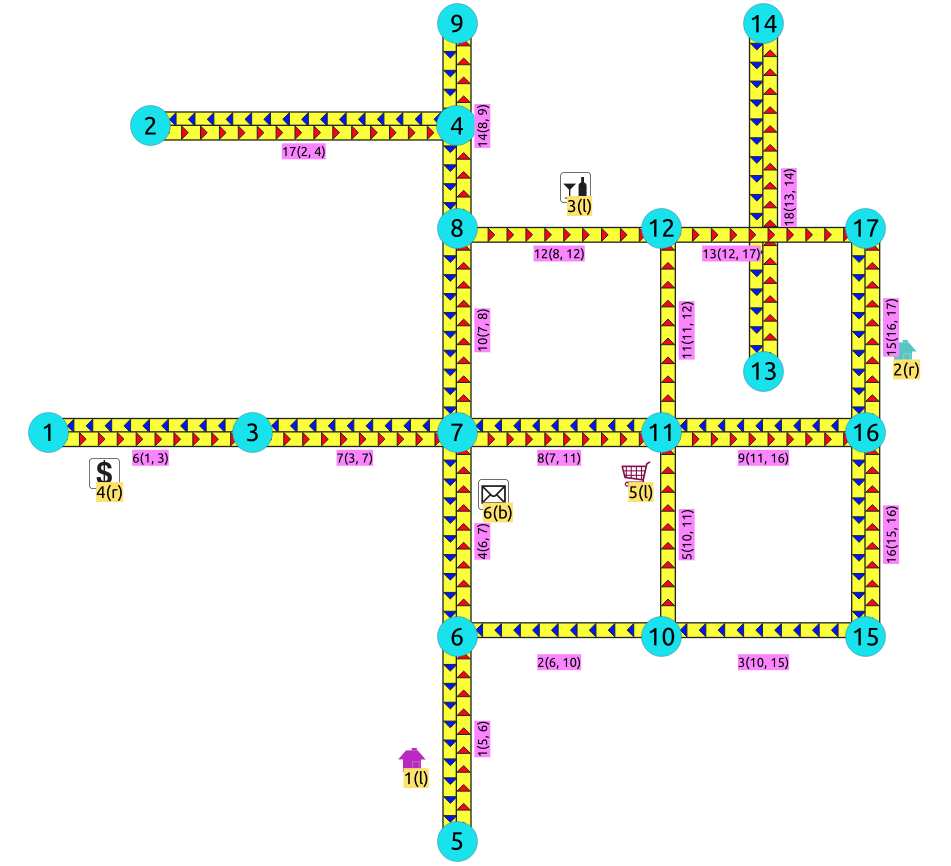
Is node \(4\) a dead end or not?

The answer to that question will depend on the application.

• Is there such a small curb:

  • That does not allow a vehicle to use that visual intersection?

  • Is the application for pedestrians and therefore the pedestrian can easily walk on the small curb?

  • Is the application for the electricity and the electrical lines than can easily be extended on top of the small curb?

• Is there a big cliff and from eagles view look like the dead end is close to the segment?

Depending on the answer, modification of the data might be needed.

When there are many dead ends, to speed up processing, the Contraction - Family of functions functions can be used to contract the graph.

Finding linear vertices

The degree of a linear vertex is 2.

If there is a vertices table already built using the pgr_extractVertices

To get the linear edges:

SELECT id FROM vertices
WHERE array_length(in_edges  out_edges, 1) = 2;
 id
----
  3
  9
 13
 15
 16
(5 rows)

These linear vertices are correct, for example, when those the vertices are speed bumps, stop signals and the application is taking them into account.

When there are many linear vertices, that need not to be taken into account, to speed up the processing, the Contraction - Family of functions functions can be used to contract the problem.