pgr_bipartite -Experimental - pgRouting Manual (3.3)

pgr_bipartite -Experimental
pgr_bipartite
- Disjoint sets of vertices such that no two vertices within
the same set are adjacent.

Warning
Possible server crash
-
These functions might create a server crash
Warning
Experimental functions
-
They are not officially of the current release.
-
They likely will not be officially be part of the next release:
-
The functions might not make use of ANY-INTEGER and ANY-NUMERICAL
-
Name might change.
-
Signature might change.
-
Functionality might change.
-
pgTap tests might be missing.
-
Might need c/c++ coding.
-
May lack documentation.
-
Documentation if any might need to be rewritten.
-
Documentation examples might need to be automatically generated.
-
Might need a lot of feedback from the comunity.
-
Might depend on a proposed function of pgRouting
-
Might depend on a deprecated function of pgRouting
-
Availability
-
Version 3.2.0
-
New experimental signature
-
Description
A bipartite graph is a graph with two sets of vertices which are connected to each other, but not within themselves. A bipartite graph is possible if the graph coloring is possible using two colors such that vertices in a set are colored with the same color.
The main Characteristics are:
-
The algorithm works in undirected graph only.
-
The returned values are not ordered.
-
The algorithm checks graph is bipartite or not. If it is bipartite then it returns the node along with two colors 0 and 1 which represents two different sets.
-
If graph is not bipartite then algorithm returns empty set.
-
Running time: \(O(V + E)\)
Signatures
- Example :
-
When the graph is bipartite
SELECT * FROM pgr_bipartite(
$$SELECT id, source, target, cost, reverse_cost FROM edges$$
) ORDER BY vertex_id;
vertex_id color_id
-----------+----------
1 0
2 0
3 1
4 1
5 0
6 1
7 0
8 1
9 0
10 0
11 1
12 0
13 0
14 1
15 1
16 0
17 1
(17 rows)
Parameters
|
Parameter |
Type |
Description |
|---|---|---|
|
|
Edges SQL as described below. |
Inner Queries
Edges SQL
|
Column |
Type |
Default |
Description |
|---|---|---|---|
|
|
ANY-INTEGER |
Identifier of the edge. |
|
|
|
ANY-INTEGER |
Identifier of the first end point vertex of the edge. |
|
|
|
ANY-INTEGER |
Identifier of the second end point vertex of the edge. |
|
|
|
ANY-NUMERICAL |
Weight of the edge (
|
|
|
|
ANY-NUMERICAL |
-1 |
Weight of the edge (
|
Where:
- ANY-INTEGER :
-
SMALLINT,INTEGER,BIGINT - ANY-NUMERICAL :
-
SMALLINT,INTEGER,BIGINT,REAL,FLOAT
Result Columns
Returns SET OF
(vertex_id,
color_id)
|
Column |
Type |
Description |
|---|---|---|
|
|
|
Identifier of the vertex. |
|
|
|
Identifier of the color of the vertex.
|
Additional Example
- Example :
-
The odd length cyclic graph can not be bipartite.
The edge \(5 \rightarrow 1\) will make subgraph with vertices \(\{1, 3, 7, 6, 5\}\) an odd length cyclic graph, as the cycle has 5 vertices.
INSERT INTO edges (source, target, cost, reverse_cost) VALUES
(5, 1, 1, 1);
INSERT 0 1
Edges in blue represent odd length cycle subgraph.
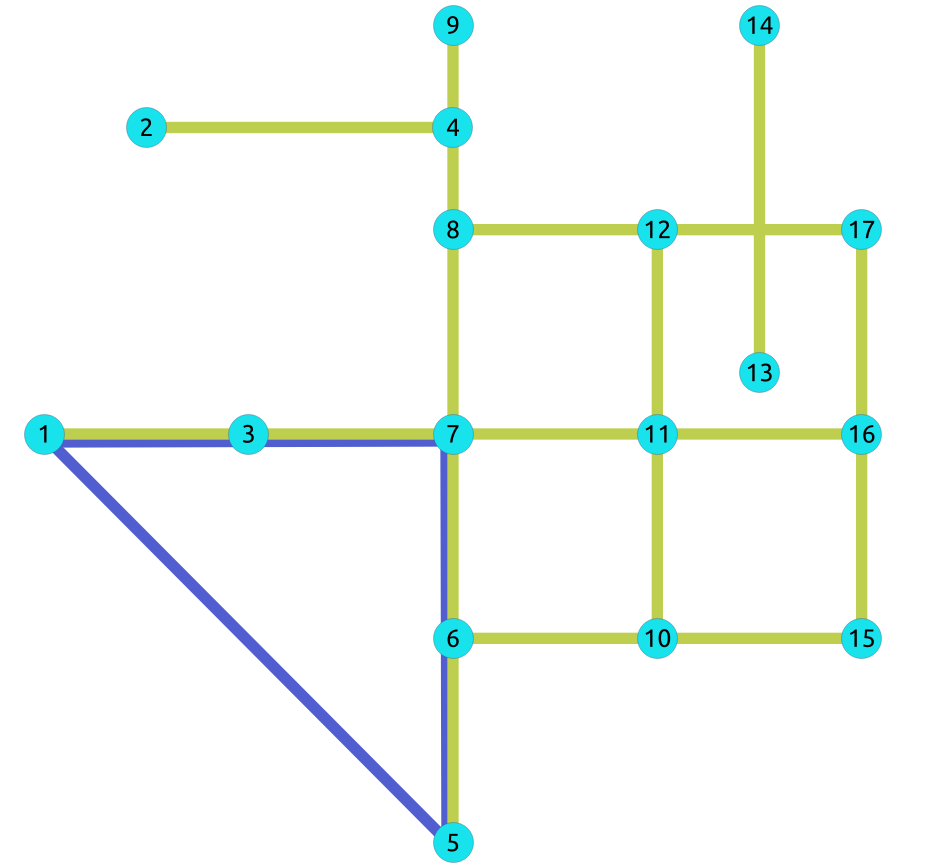
SELECT * FROM pgr_bipartite(
$$SELECT id, source, target, cost, reverse_cost FROM edges$$
);
vertex_id color_id
-----------+----------
(0 rows)
See Also
-
Sample Data network.
Indices and tables