pgr_bipartite -Experimental

pgr_bipartite - Disjoint sets of vertices such that no two vertices within the same set are adjacent.

images/boost-inside.jpeg

Boost Graph Inside

Warning

Possible server crash

  • These functions might create a server crash

Warning

Experimental functions

  • They are not officially of the current release.

  • They likely will not be officially be part of the next release:

    • The functions might not make use of ANY-INTEGER and ANY-NUMERICAL

    • Name might change.

    • Signature might change.

    • Functionality might change.

    • pgTap tests might be missing.

    • Might need c/c++ coding.

    • May lack documentation.

    • Documentation if any might need to be rewritten.

    • Documentation examples might need to be automatically generated.

    • Might need a lot of feedback from the comunity.

    • Might depend on a proposed function of pgRouting

    • Might depend on a deprecated function of pgRouting

Availability

  • Version 3.2.0

    • New experimental signature

Description

A bipartite graph is a graph with two sets of vertices which are connected to each other, but not within themselves. A bipartite graph is possible if the graph coloring is possible using two colors such that vertices in a set are colored with the same color.

The main Characteristics are:

  • The algorithm works in undirected graph only.

  • The returned values are not ordered.

  • The algorithm checks graph is bipartite or not. If it is bipartite then it returns the node along with two colors 0 and 1 which represents two different sets.

  • If graph is not bipartite then algorithm returns empty set.

  • Running time: \(O(V + E)\)

Signatures

pgr_bipartite( Edges SQL )
RETURNS SET OF (vertex_id, color_id)
OR EMPTY SET
Example :

When the graph is bipartite 

SELECT * FROM pgr_bipartite(
    $$SELECT id, source, target, cost, reverse_cost FROM edges$$
) ORDER BY vertex_id;
 vertex_id  color_id
-----------+----------
         1         0
         2         0
         3         1
         4         1
         5         0
         6         1
         7         0
         8         1
         9         0
        10         0
        11         1
        12         0
        13         0
        14         1
        15         1
        16         0
        17         1
(17 rows)

Parameters

Parameter

Type

Description

Edges SQL

TEXT

Edges SQL as described below.

Inner Queries

Edges SQL

Column

Type

Default

Description

id

ANY-INTEGER

Identifier of the edge.

source

ANY-INTEGER

Identifier of the first end point vertex of the edge.

target

ANY-INTEGER

Identifier of the second end point vertex of the edge.

cost

ANY-NUMERICAL

Weight of the edge ( source , target )

reverse_cost

ANY-NUMERICAL

-1

Weight of the edge ( target , source )

  • When negative: edge ( target , source ) does not exist, therefore it’s not part of the graph.

Where:

ANY-INTEGER :

SMALLINT , INTEGER , BIGINT

ANY-NUMERICAL :

SMALLINT , INTEGER , BIGINT , REAL , FLOAT

Result Columns

Returns SET OF (vertex_id, color_id)

Column

Type

Description

vertex_id

BIGINT

Identifier of the vertex.

color_id

BIGINT

Identifier of the color of the vertex.

  • The minimum value of color is 1.

Additional Example

Example :

The odd length cyclic graph can not be bipartite.

The edge \(5 \rightarrow 1\) will make subgraph with vertices \(\{1, 3, 7, 6, 5\}\) an odd length cyclic graph, as the cycle has 5 vertices. 

INSERT INTO edges (source, target, cost, reverse_cost) VALUES
(5, 1, 1, 1);
INSERT 0 1

Edges in blue represent odd length cycle subgraph.

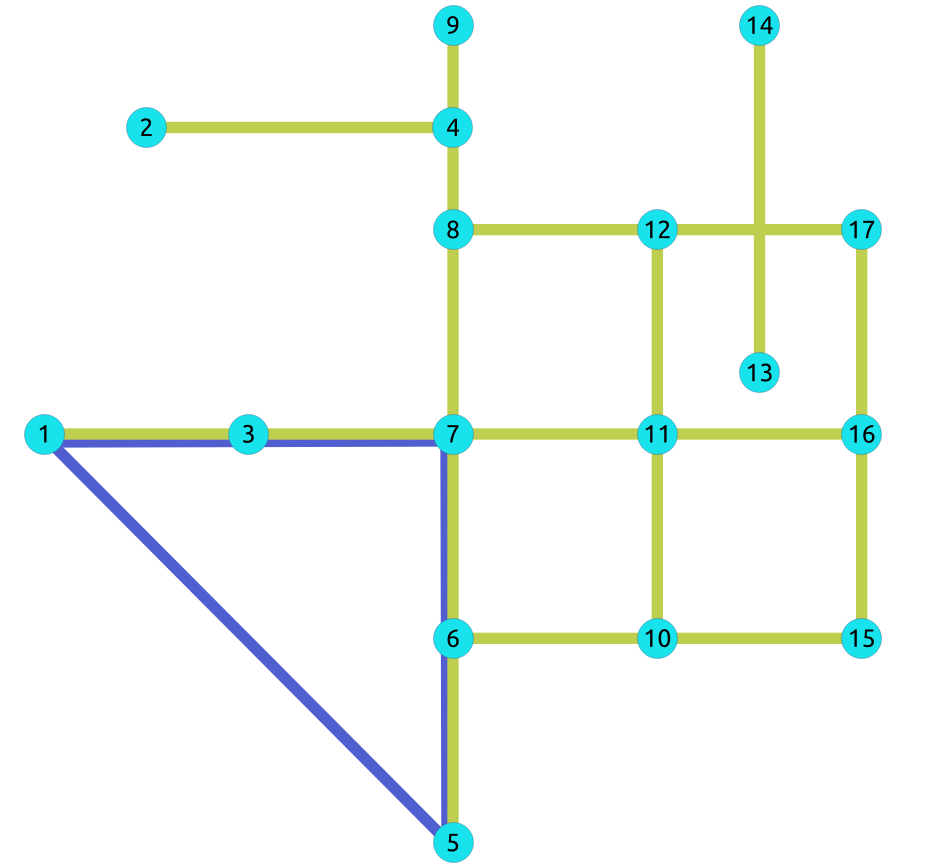
images/bipartite.png 
SELECT * FROM pgr_bipartite(
    $$SELECT id, source, target, cost, reverse_cost FROM edges$$
);
 vertex_id  color_id
-----------+----------
(0 rows)

See Also

Indices and tables