pgr_connectedComponents

pgr_connectedComponents - Connected components of an undirected graph using a DFS-based approach.

images/boost-inside.jpeg

Boost Graph Inside

Availability

  • Version 3.0.0

    • Return columns change:

      • n_seq is removed

      • seq changed type to BIGINT

    • Official function

  • Version 2.5.0

    • New experimental function

Description

A connected component of an undirected graph is a set of vertices that are all reachable from each other.

The main characteristics are:

  • Works for undirected graphs.

  • Components are described by vertices

  • The returned values are ordered:

    • component ascending

    • node ascending

  • Running time: \(O(V + E)\)

Signatures

pgr_connectedComponents( Edges SQL )
RETURNS SET OF (seq, component, node)
OR EMPTY SET
Example :

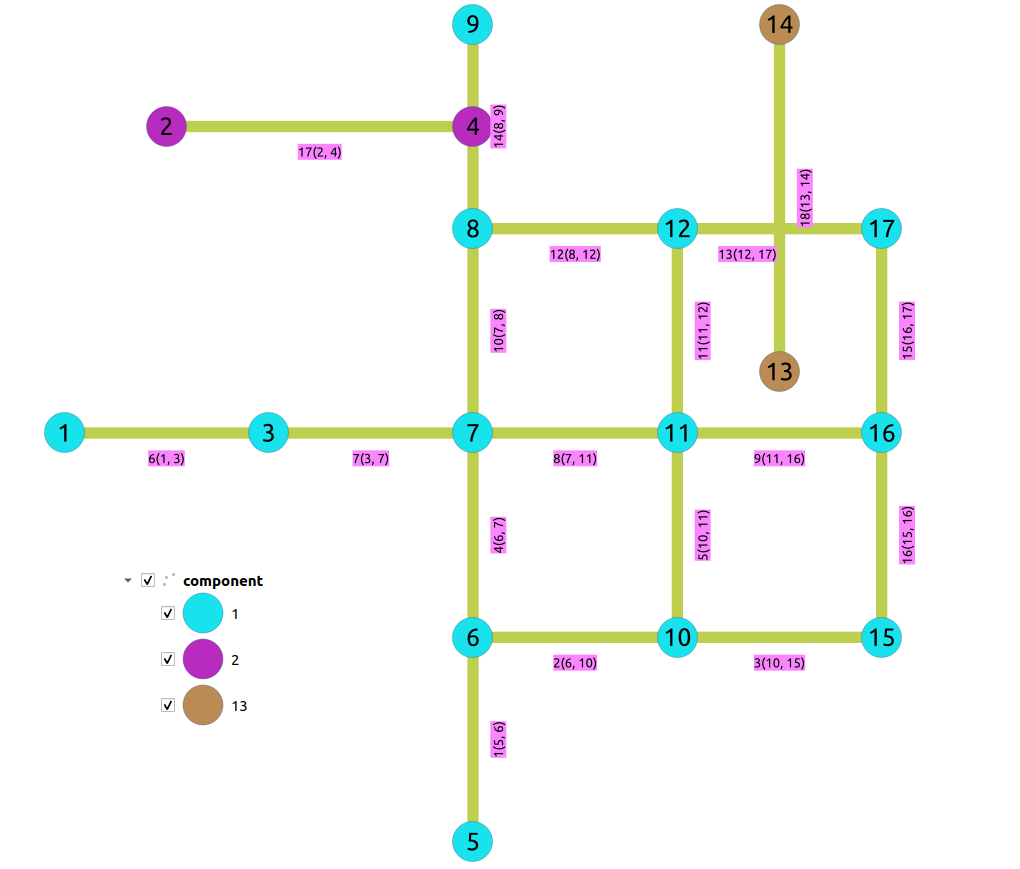
The connected components of the graph 

SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
);
 seq  component  node
-----+-----------+------
   1          1     1
   2          1     3
   3          1     5
   4          1     6
   5          1     7
   6          1     8
   7          1     9
   8          1    10
   9          1    11
  10          1    12
  11          1    15
  12          1    16
  13          1    17
  14          2     2
  15          2     4
  16         13    13
  17         13    14
(17 rows)
images/cc_sampledata.png

Parameters

Parameter

Type

Description

Edges SQL

TEXT

Edges SQL as described below.

Inner Queries

Edges SQL

Column

Type

Default

Description

id

ANY-INTEGER

Identifier of the edge.

source

ANY-INTEGER

Identifier of the first end point vertex of the edge.

target

ANY-INTEGER

Identifier of the second end point vertex of the edge.

cost

ANY-NUMERICAL

Weight of the edge ( source , target )

reverse_cost

ANY-NUMERICAL

-1

Weight of the edge ( target , source )

  • When negative: edge ( target , source ) does not exist, therefore it’s not part of the graph.

Where:

ANY-INTEGER :

SMALLINT , INTEGER , BIGINT

ANY-NUMERICAL :

SMALLINT , INTEGER , BIGINT , REAL , FLOAT

Result Columns

Returns set of (seq, component, node)

Column

Type

Description

seq

BIGINT

Sequential value starting from 1 .

component

BIGINT

Component identifier.

  • Has the value of the minimum node identifier in the component.

node

BIGINT

Identifier of the vertex that belongs to the component .

Additional Examples

Connecting disconnected components

To get the graph connectivity: 

SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
);
 seq  component  node
-----+-----------+------
   1          1     1
   2          1     3
   3          1     5
   4          1     6
   5          1     7
   6          1     8
   7          1     9
   8          1    10
   9          1    11
  10          1    12
  11          1    13
  12          1    14
  13          1    15
  14          1    16
  15          1    17
  16          1    18
  17          2     2
  18          2     4
(18 rows)

In this example, the component \(2\) consists of vertices \(\{2, 4\}\) and both vertices are also part of the dead end result set.

This graph needs to be connected.

Note

With the original graph of this documentation, there would be 3 components as the crossing edge in this graph is a different component.

Prepare storage for connection information 
ALTER TABLE vertices ADD COLUMN component BIGINT;
ALTER TABLE
ALTER TABLE edges ADD COLUMN component BIGINT;
ALTER TABLE
Save the vertices connection information 
UPDATE vertices SET component = c.component
FROM (SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
)) AS c
WHERE id = node;
UPDATE 18
Save the edges connection information 
UPDATE edges SET component = v.component
FROM (SELECT id, component FROM vertices) AS v
WHERE source = v.id;
UPDATE 20
Get the closest vertex

Using pgr_findCloseEdges the closest vertex to component \(1\) is vertex \(4\) . And the closest edge to vertex \(4\) is edge \(14\) . 

SELECT edge_id, fraction, ST_AsText(edge) AS edge, id AS closest_vertex
FROM pgr_findCloseEdges(
  $$SELECT id, geom FROM edges WHERE component = 1$$,
  (SELECT array_agg(geom) FROM vertices WHERE component = 2),
  2, partial => false) JOIN vertices USING (geom) ORDER BY distance LIMIT 1;
 edge_id  fraction                  edge                  closest_vertex
---------+----------+--------------------------------------+----------------
      14       0.5  LINESTRING(1.999999999999 3.5,2 3.5)               4
(1 row)

The edge can be used to connect the components, using the fraction information about the edge \(14\) to split the connecting edge.

Connecting components

There are three basic ways to connect the components

  • From the vertex to the starting point of the edge

  • From the vertex to the ending point of the edge

  • From the vertex to the closest vertex on the edge

    • This solution requires the edge to be split.

The following query shows the three ways to connect the components: 

WITH
info AS (
  SELECT
    edge_id, fraction, side, distance, ce.geom, edge, v.id AS closest,
    source, target, capacity, reverse_capacity, e.geom AS e_geom
  FROM pgr_findCloseEdges(
    $$SELECT id, geom FROM edges WHERE component = 1$$,
    (SELECT array_agg(geom) FROM vertices WHERE component = 2),
    2, partial => false) AS ce
  JOIN vertices AS v USING (geom)
  JOIN edges AS e ON (edge_id = e.id)
  ORDER BY distance LIMIT 1),
three_options AS (
  SELECT
    closest AS source, target, 0 AS cost, 0 AS reverse_cost,
    capacity, reverse_capacity,
    ST_X(geom) AS x1, ST_Y(geom) AS y1,
    ST_X(ST_EndPoint(e_geom)) AS x2, ST_Y(ST_EndPoint(e_geom)) AS y2,
    ST_MakeLine(geom, ST_EndPoint(e_geom)) AS geom
  FROM info

  UNION

  SELECT closest, source, 0, 0, capacity, reverse_capacity,
    ST_X(geom) AS x1, ST_Y(geom) AS y1,
    ST_X(ST_StartPoint(e_geom)) AS x2, ST_Y(ST_StartPoint(e_geom)) AS y2,
    ST_MakeLine(info.geom, ST_StartPoint(e_geom))
  FROM info
  /*
  UNION
  -- This option requires splitting the edge
  SELECT closest, NULL, 0, 0, capacity, reverse_capacity,
    ST_X(geom) AS x1, ST_Y(geom) AS y1,
    ST_X(ST_EndPoint(edge)) AS x2, ST_Y(ST_EndPoint(edge)) AS y2,
    edge
  FROM info */
  )

INSERT INTO edges
  (source, target,
    cost, reverse_cost,
    capacity, reverse_capacity,
    x1, y1, x2, y2,
    geom)
(SELECT
    source, target, cost, reverse_cost, capacity, reverse_capacity,
    x1, y1, x2, y2, geom
  FROM three_options);
INSERT 0 2
Checking components

Ignoring the edge that requires further work. The graph is now fully connected as there is only one component. 

SELECT * FROM pgr_connectedComponents(
  'SELECT id, source, target, cost, reverse_cost FROM edges'
);
 seq  component  node
-----+-----------+------
   1          1     1
   2          1     2
   3          1     3
   4          1     4
   5          1     5
   6          1     6
   7          1     7
   8          1     8
   9          1     9
  10          1    10
  11          1    11
  12          1    12
  13          1    13
  14          1    14
  15          1    15
  16          1    16
  17          1    17
  18          1    18
(18 rows)

See Also

Indices and tables