Navigation :

Table of Contents - pgRouting Manual (3.4) > withPoints - Family of functions - pgRouting Manual (3.4)

withPoints - Family of functions - pgRouting Manual (3.4)

Supported versions: Latest ( 3.4 ) 3.3 3.2 3.1 3.0
Unsupported versions: 2.6 2.5 2.4 2.3 2.2

withPoints - Family of functions

When points are also given as input:

Warning

Proposed functions for next mayor release.

They are not officially in the current release.
They will likely officially be part of the next mayor release:
- The functions make use of ANY-INTEGER and ANY-NUMERICAL
- Name might not change. (But still can)
- Signature might not change. (But still can)
- Functionality might not change. (But still can)
- pgTap tests have being done. But might need more.
- Documentation might need refinement.

pgr_withPoints - Proposed - Route from/to points anywhere on the graph.
pgr_withPointsCost - Proposed - Costs of the shortest paths.
pgr_withPointsCostMatrix - proposed - Costs of the shortest paths.
pgr_withPointsKSP - Proposed - K shortest paths.
pgr_withPointsDD - Proposed - Driving distance.
pgr_withPointsVia - Proposed - Via routing

Introduction

This family of functions belongs to the withPoints - Category and the functions that compose them are based one way or another on dijkstra algorithm.

Depending on the name:

pgr_withPoints is pgr_dijkstra with points
pgr_withPointsCost is pgr_dijkstraCost with points
pgr_withPointsCostMatrix is pgr_dijkstraCostMatrix with points
pgr_withPointsKSP is pgr_ksp with points
pgr_withPointsDD is pgr_drivingDistance with points
pgr_withPointsvia is pgr_dijkstraVia with points

Parameters

Column	Type	Description
Edges SQL	`TEXT`	Edges SQL as described below
Points SQL	`TEXT`	Points SQL as described below
Combinations SQL	`TEXT`	Combinations SQL as described below
start vid	`BIGINT`	Identifier of the starting vertex of the path. Negative value is for point’s identifier.
start vids	`ARRAY[BIGINT]`	Array of identifiers of starting vertices. Negative values are for point’s identifiers.
end vid	`BIGINT`	Identifier of the ending vertex of the path. Negative value is for point’s identifier.
end vids	`ARRAY[BIGINT]`	Array of identifiers of ending vertices. Negative values are for point’s identifiers.

Optional parameters

Column	Type	Default	Description
`directed`	`BOOLEAN`	`true`	When `true` the graph is considered Directed When `false` the graph is considered as Undirected .

With points optional parameters

Parameter	Type	Default	Description
`driving_side`	`CHAR`	`b`	Value in [ `r` , `l` , `b` ] indicating if the driving side is: `r` for right driving side. `l` for left driving side. `b` for both.
`details`	`BOOLEAN`	`false`	When `true` the results will include the points that are in the path. When `false` the results will not include the points that are in the path.

Parameter

Type

Default

Description

driving_side

CHAR

b

Value in [ r , l , b ] indicating if the driving side is:

r for right driving side.
l for left driving side.
b for both.

details

BOOLEAN

false

When true the results will include the points that are in the path.
When false the results will not include the points that are in the path.

Inner Queries

Edges SQL

Column	Type	Default	Description
`id`	ANY-INTEGER		Identifier of the edge.
`source`	ANY-INTEGER		Identifier of the first end point vertex of the edge.
`target`	ANY-INTEGER		Identifier of the second end point vertex of the edge.
`cost`	ANY-NUMERICAL		Weight of the edge ( `source` , `target` )
`reverse_cost`	ANY-NUMERICAL	-1	Weight of the edge ( `target` , `source` ) When negative: edge ( `target` , `source` ) does not exist, therefore it’s not part of the graph.

Where:

ANY-INTEGER :: SMALLINT , INTEGER , BIGINT
ANY-NUMERICAL :: SMALLINT , INTEGER , BIGINT , REAL , FLOAT

Points SQL

Parameter	Type	Default	Description
`pid`	ANY-INTEGER	value	Identifier of the point. Use with positive value, as internally will be converted to negative value If column is present, it can not be NULL. If column is not present, a sequential negative value will be given automatically.
`edge_id`	ANY-INTEGER		Identifier of the "closest" edge to the point.
`fraction`	ANY-NUMERICAL		Value in <0,1> that indicates the relative postition from the first end point of the edge.
`side`	`CHAR`	`b`	Value in [ `b` , `r` , `l` , `NULL` ] indicating if the point is: In the right `r` , In the left `l` , In both sides `b` , `NULL`

Where:

ANY-INTEGER :: SMALLINT , INTEGER , BIGINT
ANY-NUMERICAL :: SMALLINT , INTEGER , BIGINT , REAL , FLOAT

Combinations SQL

Parameter	Type	Description
`source`	ANY-INTEGER	Identifier of the departure vertex.
`target`	ANY-INTEGER	Identifier of the arrival vertex.

Where:

ANY-INTEGER :: SMALLINT , INTEGER , BIGINT

Advanced Documentation

About points

For this section the following city (see Sample Data ) some interesing points such as restaurant, supermarket, post office, etc. will be used as example.

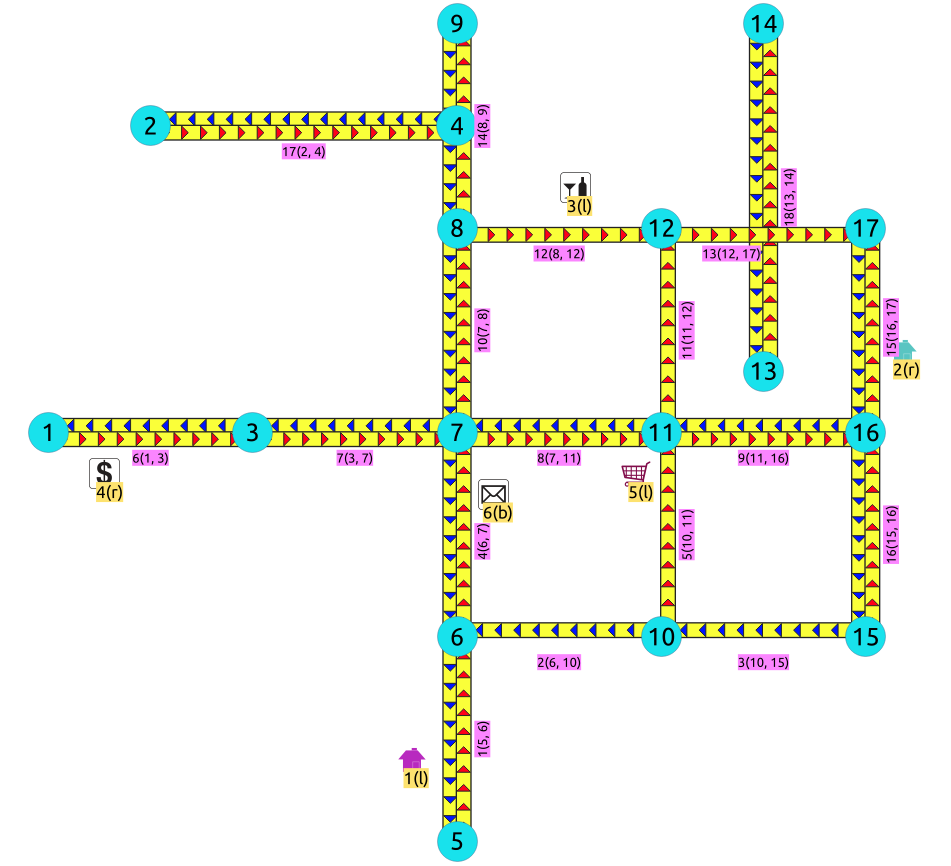
The graph is directed
Red arrows show the (source, target) of the edge on the edge table
Blue arrows show the (target, source) of the edge on the edge table
Each point location shows where it is located with relation of the edge (source, target)
- On the right for points 2 and 4 .
- On the left for points 1 , 3 and 5 .
- On both sides for point 6 .

The representation on the data base follows the Points SQL description, and for this example:

      SELECT pid, edge_id, fraction, side FROM pointsOfInterest;
 pid  edge_id       fraction       side
-----+---------+--------------------+------
   1        1                 0.4  l
   4        6                 0.3  r
   3       12  0.6000000000000001  l
   2       15  0.3999999999999999  r
   5        5                 0.8  l
   6        4                 0.7  b
(6 rows)


     

Driving side

In the the folowwing images:

The squared vertices are the temporary vertices,
The temporary vertices are added according to the driving side,
visually showing the differences on how depending on the driving side the data is interpreted.

Right driving side

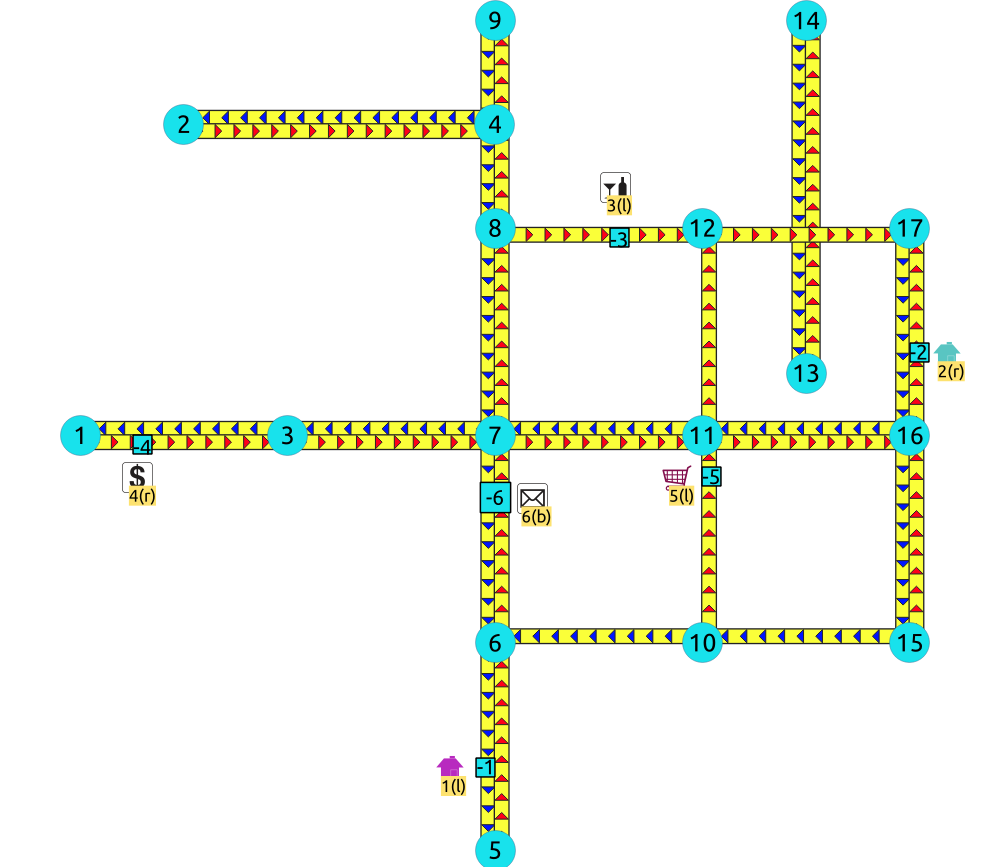
Point 1 located on edge (6, 5)
Point 2 located on edge (16, 17)
Point 3 located on edge (8, 12)
Point 4 located on edge (1, 3)
Point 5 located on edge (10, 11)
Point 6 located on edges (6, 7) and (7, 6)

Left driving side

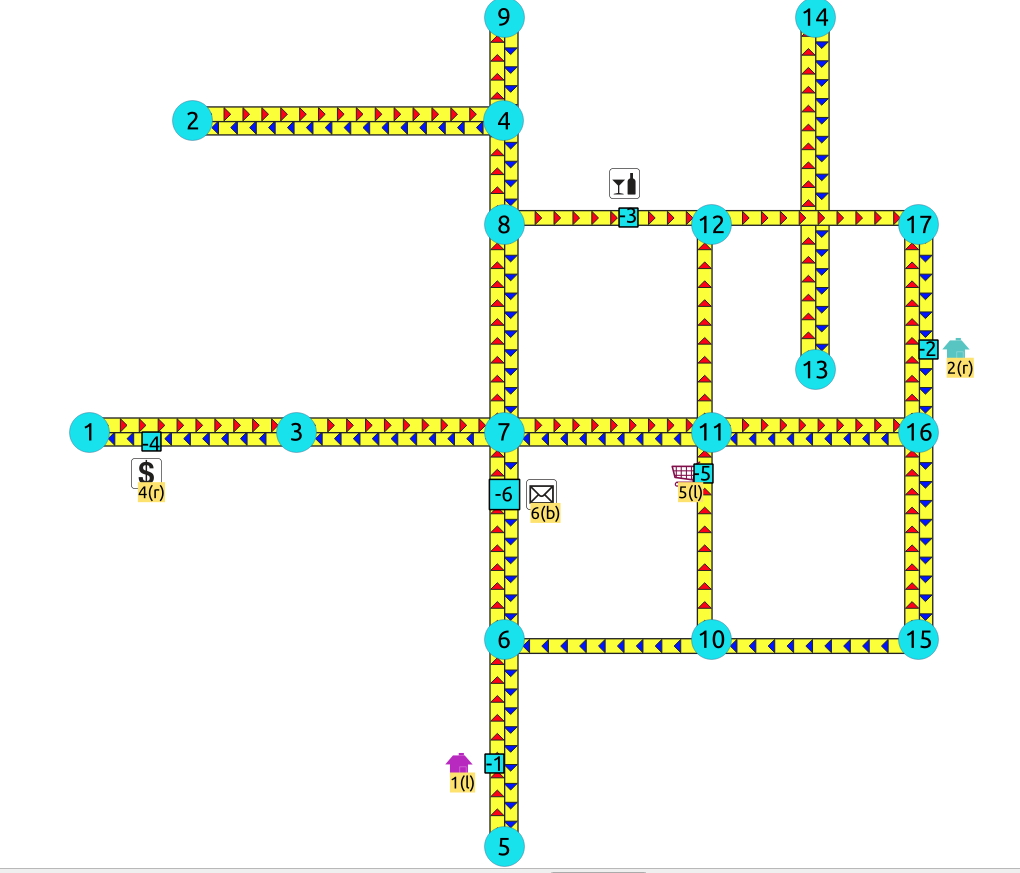
Point 1 located on edge (5, 6)
Point 2 located on edge (17, 16)
Point 3 located on edge (8, 12)
Point 4 located on edge (3, 1)
Point 5 located on edge (10, 11)
Point 6 located on edges (6, 7) and (7, 6)

Driving side does not matter

Like having all points to be considered in both sides b
Prefered usage on undirected graphs
On the TRSP - Family of functions this option is not valid

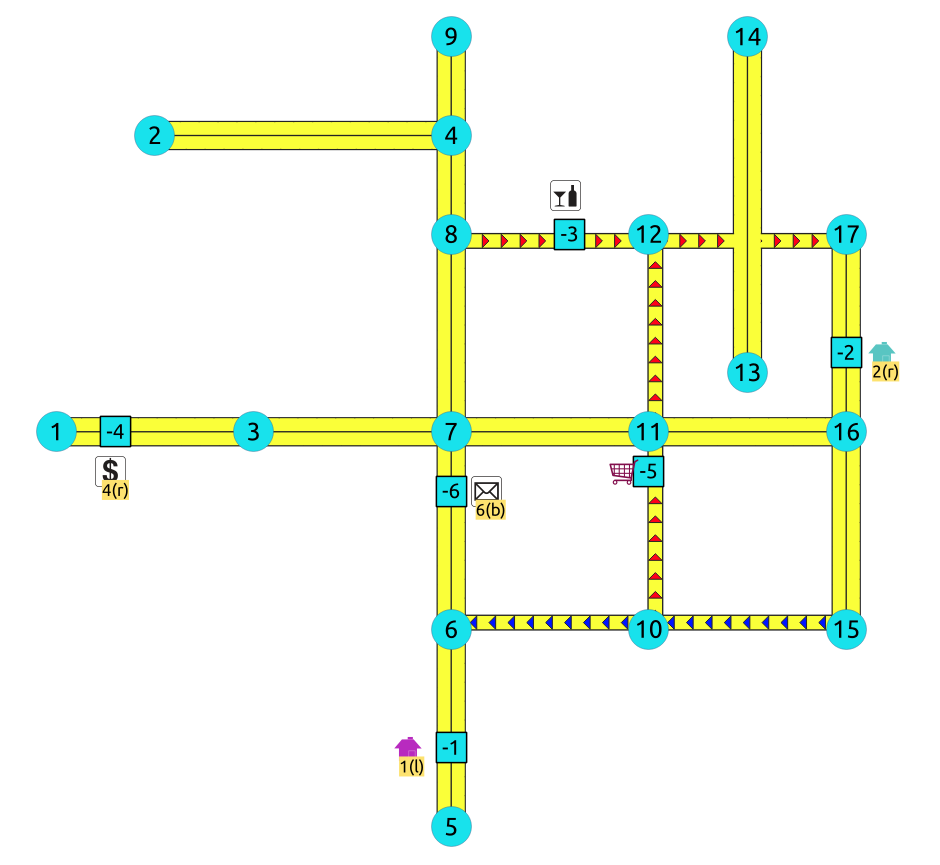
Point 1 located on edge (5, 6) and (6, 5)
Point 2 located on edge (17, 16)``and ``16, 17
Point 3 located on edge (8, 12)
Point 4 located on edge (3, 1) and (1, 3)
Point 5 located on edge (10, 11)
Point 6 located on edges (6, 7) and (7, 6)

Creating temporary vertices

This section will demonstrate how a temporary vertex is created internally on the graph.

Problem

For edge:

      SELECT id, source, target, cost, reverse_cost
FROM edges WHERE id = 15;
 id  source  target  cost  reverse_cost
----+--------+--------+------+--------------
 15      16      17     1             1
(1 row)


     

insert point:

      SELECT pid, edge_id, fraction, side
FROM pointsOfInterest WHERE pid = 2;
 pid  edge_id       fraction       side
-----+---------+--------------------+------
   2       15  0.3999999999999999  r
(1 row)


     

On a right hand side driving network

Right driving side

Arrival to point -2 can be achived only via vertex 16 .
Does not affects edge (17, 16) , therefore the edge is kept.
It only affects the edge (16, 17) , therefore the edge is removed.
Create two new edges:
- Edge (16, -2) with cost 0.4 (original cost * fraction == \(1 * 0.4\) )
- Edge (-2, 17) with cost 0.6 (the remaing cost)
The total cost of the additional edges is equal to the original cost.
If more points are on the same edge, the process is repeated recursevly.

On a left hand side driving network

Left driving side

Arrival to point -2 can be achived only via vertex 17 .
Does not affects edge (16, 17) , therefore the edge is kept.
It only affects the edge (17, 16) , therefore the edge is removed.
Create two new edges:
- Work with the original edge (16, 17) as the fraction is a fraction of the original:
  - Edge (16, -2) with cost 0.4 (original cost * fraction == \(1 * 0.4\) )
  - Edge (-2, 17) with cost 0.6 (the remaing cost)
  - If more points are on the same edge, the process is repeated recursevly.
- Flip the Edges and add them to the graph:
  - Edge (17, -2) becomes (-2, 16) with cost 0.4 and is added to the graph.
  - Edge (-2, 16) becomes (17, -2) with cost 0.6 and is added to the graph.
The total cost of the additional edges is equal to the original cost.

When driving side does not matter

Arrival to point -2 can be achived via vertices 16 or 17 .
Affects the edges (16, 17) and (17, 16) , therefore the edges are removed.
Create four new edges:
- Work with the original edge (16, 17) as the fraction is a fraction of the original:
  - Edge (16, -2) with cost 0.4 (original cost * fraction == \(1 * 0.4\) )
  - Edge (-2, 17) with cost 0.6 (the remaing cost)
  - If more points are on the same edge, the process is repeated recursevly.
- Flip the Edges and add all the edges to the graph:
  - Edge (16, -2) is added to the graph.
  - Edge (-2, 17) is added to the graph.
  - Edge (16, -2) becomes (-2, 16) with cost 0.4 and is added to the graph.
  - Edge (-2, 17) becomes (17, -2) with cost 0.6 and is added to the graph.

withPoints - Family of functions - pgRouting Manual (3.4)